
This page is a dictionary of many of the essential terms one might come across when beginning to learn group theory. Many other pages in the Group Explorer help link here to define terms. Unlike the Group Explorer terminology page, these terms are all widely known in the mathematical community.
See injective.
An abelian group is one whose binary operation is commutative. That is, for every two elements a and b in the group, a.b = b.a.
A function that is both injective and surjective is called bijective.
A Cayley diagram is a graph (that is, a set of nodes and arrows among them) which depicts a group. There is one node in the graph for each element in the group, and the arrows show how the generators act on the elements of the group. That is, if the group has two generators, a and b, then there will be one type of arrow (perhaps red-colored arrows) for generator a and another type of arrow (perhaps blue-colored) for generator b. Here is a Cayley diagram of a group; you can see that it fits this description.
The red arrows would connect two elements if multiplying the first by a gives the second; i.e.
x -----red-arrow-----> y
just when ax = y. So the arrows represent left-multiplication. (One could also make Cayley diagrams in which the arrows represented right-multiplication.)
Group Explorer has a visualizer for showing you Cayley diagrams. It is documented in full here, with an introduction here, and a tutorial here.
See multiplication table.
The elements of a group can be partitioned into conjugacy classes. The class equation is a numerical equation describing this partitioning. For instance, the group S3 has three conjugacy classes, of sizes 1, 2, and 3 respectively. The order of the group is 6, and so the class equation is
1 + 2 + 3 = 6.
All class equations are of this form: The left hand side is a sum of positive integers, each the size of a conjugacy class, and the right side the order of the group.
Not all subsets of a group are subgroups. The closure of a subset is the smallest subgroup containing that subset. That is, it answers the question, "What must I add to this subset to get a subgroup?" Another way to think of a subset's closure is that it is the subgroup for which the subset is a set of generators.
See Abelian.
The conjugacy class of an element g in a group is the set of all elements hgh-1 for any element h in the group. These are called "classes" because they partition the group (i.e. form an equivalence relation) and are called "conjugacy" classes because the element hgh-1 is called the "conjugate" of g by h.
See also class equation.
For any subgroup H of a group G, we can speak of the left cosets and the right cosets of H. The notation aH for an element a in G means the set of all products a times an element of H; this set is a left coset of H, because we multiplied by a on the left of H. One could do the same on the right, and form a right coset of H. The collection of all aH for every a in G is the collection of left cosets of H; similarly for right cosets. Cosets of either type partition the elements of the group.
A cycle graph is an illustration of the cycles of a group (orbits of elements) and how those cycles connect. Here is an example cycle graph.
The above graph shows the group Z2 x Z4. One can see that there are two four-cycles (in the bottom half of the picture) which share two nodes (the central node and the bottommost node). In addition to these six elements, there are two other order-2 elements that are not in either of the two larger four-cycles, shown at the top of the picture.
Group Explorer has a visualizer for showing you Cycle graphs, documented in full here.
A cyclic group is one that is generated by one element. Therefore it is comprised entirely of the orbit of that element. The Cyclic groups are denoted Zn or sometimes Cn, and look just like their name (cycles) when viewed as Cayley diagrams or cycle graphs.
One can define groups by listing generators a, b, c, ... and then writing equations that describe how they relate. For instance, the cyclic group with five elements can be described as the group generated by a where a5 is the identity element. This is written < a : a5 = e >. The portion to the left of the colon (:) is the lone generator a and the portion to the right is the equation that describes it.
For groups with more than one generator, the situation is slightly more complex, but is essentially the same. The definition < a, b : a4 = e, b2 = e, ab = ba > describes a group with an order-4 generator a and an order-2 generator b which commute with each other. The last equation ab = ba describes the commutativity of the generators, and therefore implies the commutativity of the whole group. This group is thus Z2 x Z4. But if we had written the same definition with a different final equation, say , we would have come up with a different group (D4).
One of the columns available for view in the main window (the group library) is the definition in this format of every group loaded.
The elementwise product of two subsets S and T of a group is written ST and is the set of all products of elements from S with elements from T, in that order. Thus the product is taken on the level of elements, or "elementwise." In set theory notation, ST =
See surjection.
The First Isomorphism Theorem says that given a homomorphism f mapping a group G to a group G', the kernel of f is a normal subgroup of G, and when we take the quotient G/Ker(f), it is isomorphic to the image Im(f) as a subgroup of G'.
This is useful in short exact sequences, which Group Explorer uses to illustrate the normality of subgroups. (To see an example, open a group info window, click the "tell me more" link next to the Subgroups computation, and search for "short exact sequence" on that page--it will be in the description of any normal subgroup.)
A collection C of elements of a group is said to generate the group (and they are called generators) if all possible combinations of multiplications of those elements with one another yields all elements of the group.
For instance, the elements r and f in S3 generate the group because the complete list of elements of S3 is r, f, rf, fr, r2, plus the identity, which can be written as r3. Thus all elements of S3 are expressible as products of r's and f's, so the set
If we consider just the element r in the same group, and ask what set of elements it generates, < r >, we find only the elements
A group is a set of elements together with a binary operation (which I'll denote here by *) such that the following criteria hold.
But this is the dry, boring definition of a group! You should be out looking at pictures of them! That's what this program is for!
Sometimes called simply a morphism, this is a function from one group to another--that is, from the set of elements of the one group to the set of elements of the other. However, it must not be simply a function, it must also preserve the group operation. That is, it must keep the group's structure intact in the following specific way: For every pair of elements a and b in the domain, the homomorphism f must satisfy the equation f(ab) = f(a)f(b). "Homomorphism" means "same shape/form" (homo = same, morph = shape/form).
If a homomorphism f maps group G to group G', and there is a subset S of G, we can find out what its "image" is under the homomorphism f by simply applying f to each element of S. That is, the image of S under f, sometimes written f[S], is the set
One can also speak of the image of f, meaning the image of the whole group G under f, i.e. all elements of the codomain of f.
See also preimage.
The order of a subgroup will always divide the order of the group. So we say that a subgroup's index is the integer resulting from that division. In symbols, if H is a subgroup of G, then because |H| divides |G|, the index is |G|/|H|, often written [G:H].
A function is injective (or 1-1, or an injection) if no two different elements map to the same thing. That is, if a and b are not equal, then f(a) and f(b) are not equal either. An injective homomorphism is sometimes called a monomorphism.
A homomorphism that is both bijective is called an isomorphism. In group theory, if there is an isomorphism from one group to another, that means that those groups are really the same exact structure, but possibly with different names or labels. In other words, they are the same mathematical object.
Oftentimes people do not consider the distinction of labeling significant, and will therefore call two objects the same if they are isomorphic. This is what is meant by the phrase "the same up to isomorphism"; it means the things are the same if we consider isomorphic things to be identical.
The First Isomorphism Theorem can be illustrated in Group Explorer. Other isomorphism theorems do not yet appear illustrated in this software.
The kernel of a homomorphism is the set of elements which the homomorphisms maps to the identity element. Sometimes written Ker(f), this set is the preimage of the set
I will not define the concept of a lattice here; it is too deep a subject for the small need we have of it. One can find a good definition of it in a discrete mathematics textbook, or an online resource like MathWorld or Wikipedia.
For our purposes, a lattice is a two-dimensional arrangement of sets, with larger objects higher in the arrangement (vertically), and with arrows drawn from smaller objects up to larger ones if the smaller object is a subset of the larger. Because all subgroups of a group are sets, we can arrange them in a lattice. For example, click here to see the lattice of subgroups of S3 (illustrated using multiplication tables).
See cosets.
See injection.
See homomorphism.
A multiplication table for a group is named thus because it is much like elementary school multiplication tables, except that it uses the group elements and operation rather than integers under ordinary, everyday multiplication.
Thus the table is a grid, and across the top row and down the left column every element of the group is listed, and filling the rest of the table is the results of applying the group operation to the elements in the header row and column. For this reason, multiplication tables very well exhibit patterns inherent in the group operation, but elements themselves appear several times in the table, and thus the group as a set is not well depicted.
Group Explorer has a visualizer for showing you multiplication tables. It is documented in full here, with an introduction here, and a tutorial here.
Group Explorer shows multiplication tables in one of two ways--with or without text in the cells of the table. Consider the following multiplication table for the group D4.
This table has no text, and thus the colors of the cells exhibit the abstract pattern inherent in the group operation. Omitting the text from the table allows tables to be shown in small sizes (like in group info pages or the group library). If you want to see this same table with the element names in the cells, click on the above table (to open the group info page for D4) and then click the multiplication table visualizer shown under the Views section. (If you don't want to go through all those steps, just click here.)
Upon inspecting the multiplication table with text included, you can see that for example the element r in the leftmost column, second row, multiplied by the element f (in the topmost row, fifth column) results in the element rf, in the second row, fifth column. This is because multiplication is done in the order you can infer from this example: element in left column times element in top row.
A subgroup is called normal when any of the following equivalent criteria are met.
The last of these is probably the easiest to visualize. Multiplication tables and Cayley diagrams can both organize themselves by the cosets of a subgroup and then separate those cosets (or "chunk" them) to help you visualize the quotient operation. Refer to the documentation on the multiplication table interface or the Cayley diagram interface for more information on these features.
The normalizer of a subgroup H of a group G, sometimes written Norm(H), is the largest subgroup containing H in which H is normal.
That is, H may not be normal in G, but if we were to remove some of the "problem" elements from G, those that are preventing H from being normal, we would find a subgroup of G in which H is normal. The normalizer is exactly this, the subgroup which remains when you remove as few elements as possible from G to make H normal.
Group theory is the study of symmetry in the abstract. But many very concrete objects which one could hold in one's hand have symmetry (or symmetries) to them, and the relationship among those symmetries can be described by a group. Therefore several groups in Group Explorer's library are groups that describe the symmetry of objects that exist in three-dimensional space, and exist in the real world--for example, a cube, a pinwheel, or a pyramid. These objects are called "objects of symmetry" (or objects with symmetry, or symmetry objects).
Group Explorer has a visualizer for showing you objects of symmetry, documented in full here.
A note for users who have upgraded from Group Explorer 1.5.8: Objects of symmetry can no longer be navigated rigidly using group operations as they could in version 1.5.8. This enhancement is planned for a future release in the version 2.0 series.
See injective.
See surjective.
The orbit of an element a in a group G is the set of all powers of that element, i.e.
Each element in a group has an order, and thus we can partition the elements of the group into classes which all have the same order. For instance the elements of the group S3 are listed in the table below, with their orders.
| Element | e | r | r2 | f | fr | rf |
| Order | 1 | 3 | 3 | 2 | 2 | 2 |
Thus this group has three order classes: one consisting of the elements of order 1,
You can learn about the order classes of any group by looking under the Computations section of its group info page.
The order of an element in a group can be thought of in two equivalent ways.
The order of the identity element is 1 by either of these reckonings. It generates the subgroup
The order of a group G, written |G|, is simply its size (how many elements are in it).
The order of a subgroup H, written |H|, is simply its size (how many elements are in it). See also subgroup index.
A p-subgroup is a subgroup all of whose elements have an order equal to a power of the prime number p. (See also Sylow p-subgroup.)
For instance, if every element of H has order 1, 2, 4, 8, 16, ... (any power of 2), then H is a 2-subgroup. If every element of H has order 1, 5, 25, 125, ... (any power of 5), then H is a 5-subgroup. One does not say "4-subgroup" or "20-subgroup" because those numbers are not prime. Also, one can see that if H is a p-subgroup for some prime p, then it is not a q-subgroup for any other prime q unless H =
If you click "tell me more" next to Subgroups in the Computations section of any group info window, you will see that the descriptions of the subgroups tell you which ones are p-subgroups.
If a homomorphism f maps group G to group G', and there is a subset S of G', we can find out what its "pre-image" is under the homomorphism f by finding all the elements which f maps into S. That is, the preimage of S under f, sometimes written f-1[S], is the set
A subgroup is proper if it is not the whole group.
That is, technically by the definition of subgroup, every group is a subgroup of itself. But when we say "a proper subgroup" we mean subgroups that are actually smaller than the group we're looking inside.
If H is a subgroup of G, then we can make a group out of the cosets of H as follows. The cosets of H (let's use the left cosets) are the sets aH for various values of a. To define an operation on this collection, we let aH times bH equal (ab)H. One can prove that this operation is a valid group operation (as per the definition of a group) if and only if H is a normal subgroup of G. In that case, the new group we just formed is called the quotient of G by H, written G/H.
Multiplication tables and Cayley diagrams can both organize themselves by the cosets of a subgroup and then separate those cosets (or "chunk" them) to help you visualize the quotient operation. Refer to the documentation on the multiplication table interface or the Cayley diagram interface for more information on these features.
See cosets.
An exact sequence is a chain of groups connected by homomorphisms such that the image of any one homomorphism in the chain is the kernel of the next homomorphism. A short exact sequence is one with only five groups in it, the first and last of which are both the trivial group. An example is shown below.
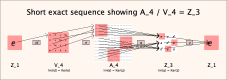
A short exact sequence is related to the quotient operation on groups. Let us call the four morphisms in a short exact sequence id, e, q, and z, from left to right, and the three middle groups in the sequence A, B, and C, also from left to right.
I call the first homomorphism id (for "identity") because it simply maps the one element in its domain (the identity element) to the identity element in A. As per the definition above, the kernel of e must be the image of id, which is simply the identity element. A nice theorem of group theory tells us that when a morphisms' kernel is the identity, the whole morphism is embedding; thus a copy of A appears in B, that copy being the image of e (for "embedding"). In turn, the kernel of q must be the image of e, which is an isomorphic copy of A. This means that the map q effectively zeroes out/removes A from B. The First Isomorphism Theorem then implies that q is a quotient map (hence the q) and that B/A = Im(q). But there's more! Because the image of z is only the identity element, its kernel is all of C. Therefore because this is an exact sequence, the image of q must also be C. This means that the short exact sequence A-->B-->C illustrates the fact that B/A = C.
You can see a short exact sequence illustrated for any normal subgroup of any group. Go to a group's info window, to the Subgroups section under Computations, and click "tell me more." Any normal subgroup will provide a link to a sheet illustrating the quotient via a short exact sequence.
A simple group is a non-abelian group with no non-trivial, proper, normal subgroups. The smallest simple group is A5.
Solvable groups are important in Galois theory, which is too large a topic to embark on here. Briefly, Galois theory was invented to study which polynomials are solvable using ordinary arithmetic plus square roots (and cube roots, etc.). If you are interested in Galois theory, refer to an abstract algebra textbook, or an online resource such as MathWorld or Wikipedia.
The roots of polynomials have symmetry that can be described by groups, called the Galois group of the polynomials. Evariste Galois (a 19th century mathematician) proved that you could tell by looking at these groups whether the polynomial was solvable. Groups that corresponded to solvable polynomials got the name "solvable groups."
A group G is solvable if there is a chain of groups H1, H2, H3, ..., Hn such that each group is a normal subgroup of the next one in the chain, the resulting quotient groups are all abelian, and the chain begins with the trivial group and ends with G. You can see a diagram illustrating this for any solvable group by looking under the Computations section of the group's info window.
If S is a subset of the group G (i.e. a subset of the set of elements of G) then we say S is a subgroup if it is also a group under the operation of G.
A subset S of a group G may fail to be a subgroup in a few different ways; here are examples. If S does not contain the identity element, it violates one of the criteria in the definition of a group. If S contains an element but not that element's inverse, it would violates another of those criteria. If S contains two elements but not their product, then the binary operation of G cannot really be said to be a binary operation on S, because it maps some pairs from S outside of S.
A function is surjective (or onto, or a surjection) from a set A to a set B if every element of B is mapped to by some element of A. That is, if b is in B, then there must be some a in A such that f(a) = b. A surjective homomorphism is sometimes called an epimorphism.
A Sylow p-subgroup is a maximal p-subgroup; i.e. no subgroup containing this one is still a p-subgroup.
If you click "tell me more" next to Subgroups in the Computations section of any group info window, you will see that the descriptions of the subgroups tell you which ones are Sylow p-subgroups.
See objects of symmetry.
The trivial group is the group with only one element. You can see its information here.
In every group, the set containing only the identity element is a subgroup, and is called the trivial subgroup.
Quick help links:
Contents | Getting Started | Tutorials | User Manual | Miscellaneous Reference
GE terminology | Help on help